Bitcoin Proof-of-Work (PoW): A Detailed Guide

🍊 Found this valuable?

🎓 Ready to Test Your Knowledge?

Subscribe for free so you don't miss our next article!

If you've heard of bitcoin before, you may have heard of proof-of-work (PoW).

After reading this article, you'll understand:

• What it is
• Why it's important
• How it works

Real Life Examples

The easiest way to understand the term "proof-of-work" is to look at examples of it in everyday life:

1. Imagine a house with a lawn. The grass on that lawn will eventually grow long unless someone regularly trims it. Therefore, if you see this lawn is freshly trimmed, you know that it was mowed. You don't need more evidence because you can tell just by looking at it.
   
   You could call this proof-of-mowing.
   
2. Now imagine a piece of paper with some words on it. In order for those words to appear on the paper, someone had to write on it. Therefore, if you see this paper has words on it, you know someone (or something) was writing.
   
   You could call this proof-of-writing.

Work

Both of the above––lawn mowing and writing––are examples of proof-of-work. But what exactly is "work"?

In bitcoin and computing systems generally, work refers to energy that has been spent, usually measured in watts. When a person walks across a room, they work to move each leg by spending caloric energy. Similarly, when a handheld calculator solves a simple math problem (e.g. 100+100), it works to find the answer by spending electrical energy.

Adding More Work

Such a small amount of work is often unnoticeable because it happens quickly and costs almost nothing. But what happens if you add more work?

Ask a person to walk one trillion miles or a calculator to find every digit of π, and in both cases the vast amount of work will be too much to handle. At some point, more work becomes too costly to complete for the worker, whether it is a human being or a computer. This is because all work requires energy, which is a finite resource. No matter how hard you try, you cannot create more energy out of nothing. This is the law of conservation of energy and it is a law of nature.

Hashcash

In 1997, a British cryptographer named Adam Back realized he could use this simple fact of nature––that energy, or work, is costly and finite––to fight spam. At the time, email spam in particular was a serious problem plaguing the early Internet. Spammers had every incentive to spam because there was no cost to send millions of emails with malicious links. Even if only 0.1% of recipients clicked the links, that strategy was still profitable for the spammer.

To combat this, Back developed a system that imposed a small computational cost on the sender of any email. Honest users were unaffected, because the cost to send one email was unnoticeable. However, spammers were eliminated because the cumulative cost to send one million emails, for example, would be far too great to bear for the spammer. This was the first major implementation of proof-of-work in distributed computing systems.

While Back's Hashcash didn't survive for very long, his innovation with proof-of-work was critical. Roughly a decade later, it served as a key ingredient in the first successful cryptocurrency: Bitcoin.

Bitcoin

In 2008, on an online forum of mostly anonymous programmers and cryptographers known as "cypherpunks", an unknown entity by the name of "Satoshi Nakamoto" published a now famous paper titled Bitcoin: A Peer-to-Peer Electronic Cash System. Back's Hashcash was cited as one of the eight references at the end of the paper.

Nakamoto took Back's idea for proof-of-work and used it in an entirely new way. Instead of requiring users of the Bitcoin network to complete proof-of-work, which would have been similar to Back's cost requirement on email senders in Hashcash, Nakamoto envisioned a system of money where anyone could broadcast their transactions to the network but only those who completed a valid proof-of-work could officially add those transactions to the permanent ledger (the blockchain).

Individuals in this group, known as miners, compete with each other in a hashing race (explained below) for the privilege to add groups of transactions (blocks) to the blockchain. In return, they collect transaction fees and bitcoin rewards from the network.

Hashing

What made Adam Back's proof-of-work novel, and likely a big reason Nakamoto incorporated it into Bitcoin, is that it forced participants to do a very specific type of work called hashing. Crucially, unlike other types of computational work such as solving difficult math problems, hashing is random, so a fast computer won't always win against a slower one.

Lottery Example

This is similar to a lottery contest. If Bob buys 10,000 lottery tickets but Alice only buys one, Bob's chances of winning are higher but Alice could still win the jackpot!

Demo

1. Open this hashing demo web page
2. Type anything––anything at all––into the box on the page
3. Notice how the string of letters and numbers (called the "hash") underneath the box changes

What you've done above is called hashing. Every input you type creates a random hash. A hash is like a fingerprint for whatever data you input.

Try This

1. Type Word into the box. You'll get this hash:
   3a2860ece5a4ee0b48b41ee96dd8054cf9bc6f113249ec601478b2582d72ead4

2. Next, type word into the box (lowercase 'w'). You'll get a different hash:
   98c1eb4ee93476743763878fcb96a25fbc9a175074d64004779ecb5242f645e6

3. Finally, re-type Word into the box, same as step 1, and you'll get this:
   3a2860ece5a4ee0b48b41ee96dd8054cf9bc6f113249ec601478b2582d72ead4

Notice how hash #1 and hash #3 above are identical because their inputs are identical, and all three hashes are the same length. Translated into bits (the smallest unit of data in computing representing either a '0' or a '1'), each output above is 256 bits long.

Challenge

The first three people to complete this challenge and tag us on Twitter (@clementinemoney) with a valid input will receive rewards of 3,000 sats each!

Try to find an input that creates a hash with these characteristics:

1. It must be 256 bits long (just like the ones above)
2. The first two characters must be zeros

Can you do it?

If you found one, great job! You just successfully mined for a specific target hash by putting in work. Be sure to tag us on Twitter with your valid input as your proof-of-work, and we'll send you a reward!

Now, let's take a look at why proof-of-work is so important for bitcoin.

The proof-of-work chain is a solution to the Byzantine Generals' Problem.

– Satoshi Nakamoto, 2008

The Byzantine Generals' Problem

Known as the "hard problem" of distributed data processing, the Byzantine Generals' Problem is a thought experiment used to illustrate a seemingly impossible coordination problem between individuals in a distributed computing network. At least, it appeared to be impossible in practice... until Bitcoin.

The Setup

Several Byzantine generals surround an enemy city, each with a small army. In order to attack and emerge victorious, all armies must attack at the same time. However, they are separated by long distances and lack instant communication.

To coordinate, the generals can try to send messengers to each other with their proposed attack times. However, there is a risk that messengers will get intercepted by the enemy. If this happens, messages may never be delivered, or worse yet they could be replaced with fake ones by the enemy.

Generals represent computers on a distributed network, messengers represent data packets sent between computers, and messages are the information inside.

Applied to Bitcoin

The main goal of bitcoin was to create money that is decentralized and reliable despite a hostile environment. Just like the generals in the Byzantine Generals' Problem coordinating to agree on a specific attack time, computers on the Bitcoin network must coordinate somehow to agree on a specific transaction history.

Even though signals travel quickly between computers, there is still significant delay across distances and the constant threat of hostile actors trying to intercept messages or somehow cheat the system.

To address this coordination problem, bitcoin uses proof-of-work.

Satoshi's Vision

In this email archive from the Cryptography Mailing List in 2008, Nakamoto eloquently explained how proof-of-work solves the Byzantine Generals' Problem.

As a brief overview: Instead of relying exclusively on sending data packets (messengers), Nakamoto designed bitcoin so that mining nodes (generals) on the Bitcoin network race to produce provably difficult hashes (proofs-of-work) as soon as they receive new blocks (messages) from other nodes. Within their new blocks, miners include the hash from the previous block they just received, thus linking each new block to the one before it in a deterministic relationship. Because nodes on the network can easily validate the difficulty of each proof-of-work attached to each block, consensus can be achieved without instantaneous communication.

This whole process helps to achieve what is now called "Nakamoto Consensus".

Nakamoto Consensus

Also known as the "longest chain rule", Nakamoto Consensus refers to the golden rule all bitcoin nodes follow when deciding on the true state of the ledger. Put simply, the rule is as follows: the longest chain always wins.

If two miners mine on top of different blocks and thus produce separate blockchains, then the longest chain will always be chosen by anyone deciding which block to mine on top of next. Eventually, due to the random nature of hashing, a longest chain will always emerge, which creates consensus.

Difficulty

The key to Satoshi's vision is that it must always take a sufficiently long amount of time and work on average to find a valid proof-of-work.

This is known as difficulty and it is crucial for consensus in bitcoin. If proofs-of-work are set to be very difficult and time-consuming to produce, then whenever a new one is broadcast to the network, all participants will easily see that sufficient work was performed and a longest chain will emerge. Instead, if proofs-of-work are too easy, then blocks could be produced in quick succession (e.g. every second), flooding the network with blocks and making it harder to find the longest chain.

The Difficulty Adjustment

As technology improves over time, computers get faster and cheaper. The average smartphone today is millions of times more powerful than the computers NASA used in the 1960's to send humans to the moon!

Therefore, as computer efficiency improves over time, the Bitcoin network needs to adjust proof-of-work difficulty to compensate. Specifically, Nakamoto designed Bitcoin so that it always takes ten minutes on average for the network to find a new proof-of-work. To accomplish this, the network recalibrates difficulty every 2,016 blocks (which equates to roughly every two weeks).

How It Works

Recall the challenge from the first section of this article. You had to find a hash with just two leading zeros. To increase the difficulty of that challenge, we could change the rule as follows: now you have to find a hash with three leading zeros. That will take more time to find because it's a more specific hash pattern.

Analogy

The difficulty adjustment is like a game of limbo. Whenever mining power increases (or decreases) over a two-week period compared to the goal of ten-minute average block times, the network lowers (or raises) the "limbo bar" by lowering (or raising) the target hash. This makes the target hash harder (or easier) to generate. This adjustment happens automatically, roughly every two weeks.

Example

A target hash could have ten leading zeros, or 15, or more! Each additional leading zero effectively means the target hash is getting smaller, because a hash is really just a number. That might seem strange because it can be represented by your computer as a text string, like this:

3a2860ece5a4ee0b48b41ee96dd8054cf9bc6f113249ec601478b2582d72ead4

But really, that is a 256-bit number and it's larger than this one with leading zeros:

00000000000000000000a62527fc5ce6f19673b637714df28ebc92348306cdd7

The above is a real hash from Block #749,144. It has 20 leading zeros, which means it probably took a lot of work to find!

Demo of the Difficulty Adjustment

Click and drag the bitcoin logo (your target hash) on the following axis:

• The target hash set by the bitcoin network can be any value along this axis.
• There are 2^256 values along the axis (roughly equal to the number of atoms in the perceivable universe).
• Green values represent valid proofs-of-work, because they're smaller than the target hash.
• Remember: Generating hashes is just guessing numbers. It's completely random.

Try This

1. Drag the bitcoin logo to the right. What have you done?
   
   Answer: You decreased the difficulty. See how the green bar expanded? That's because now a greater percentage of possible guesses are valid.
   
   More valid guesses means you're more likely to find one, so the puzzle is now easier.
   
   
2. Now drag the bitcoin logo to the left. What have you done?
   
   Answer: You increased the difficulty. The green bar shrunk, because now a smaller percentage of possible guesses are valid.
   
   Fewer valid guesses means you're less likely to find one, so the puzzle is now harder.

Now that you conceptually understand proof-of-work, hashing, consensus, and difficulty, let's take a look at how bitcoin mining actually works in detail!

Bitcoin mining uses proof-of-work. Below, we'll detail the process in five steps!

Step 1: The Setup

A bitcoin miner typically has two things set up from the start:

1. A mining node
2. A mining ASIC (Application Specific Integrated Circuit)

A node is any computer that runs a copy of the open source Bitcoin Core software and keeps a history of bitcoin transactions. It is connected to the peer-to-peer Bitcoin network, which means it is constantly receiving, validating, and relaying bitcoin transactions and blocks in real-time as they are broadcast by bitcoin users and other nodes. This entire process is automated and follows simple mathematical rules, requiring no human involvement.

A mining ASIC is a specialized device that is very good at one thing: hashing. Just like a node, a mining ASIC simply follows an automated process and requires no human involvement. The ASIC is connected to the node, which sends instructions.

Step 2: The Mempool

First, a bitcoin user somewhere in the world makes a transaction. For example:

Bob sends 1 BTC to Alice, with 0.00001 BTC in mining fees

Bob's bitcoin wallet (an application on his phone) broadcasts these transactions to nodes on the Bitcoin peer-to-peer network. Each node that receives the message from Bob's wallet checks to make sure the transactions are valid by running a series of automated mathematical functions.

Once validated, nodes add Bob's transactions to their respective mempools. The mempool is like a waiting room for validated bitcoin transactions where they sit until they are added into a block by a miner.

Step 3: The Candidate Block

Meanwhile, a bitcoin miner somewhere in the world begins to assemble a block. We'll call this miner Mallory.

Mallory is completely unaware of Bob's transactions sitting in the mempool. However, she would like to earn some bitcoin by mining. Whenever a block is produced by a miner, that miner broadcasts the block to the whole network. So, once Mallory's mining node receives the latest block from the network (call it: Block #20), the race is on to find a valid target hash for the next block (Block #21).

First, Mallory's node must validate Block #20. After all, there is no reason to build on top of an invalid block, as it will be 100% guaranteed to be rejected by the network. (Remember: these rules of validity are all automated and based on math).

Next, Mallory's mining node constructs a candidate block.

The Block

Mallory's candidate block is very simple. It contains two basic elements:

1. Block Header
   
   The block header contains six fields (shown below). We won't cover all of them in this article, but each one records important data about the block.
   
2. Coinbase Transaction
   
   The coinbase transaction is the first transaction in the block and it pays out the bitcoin reward to the miner. By including this, Mallory is basically writing herself a check for the current bitcoin reward, which is 6.25 BTC as of writing.

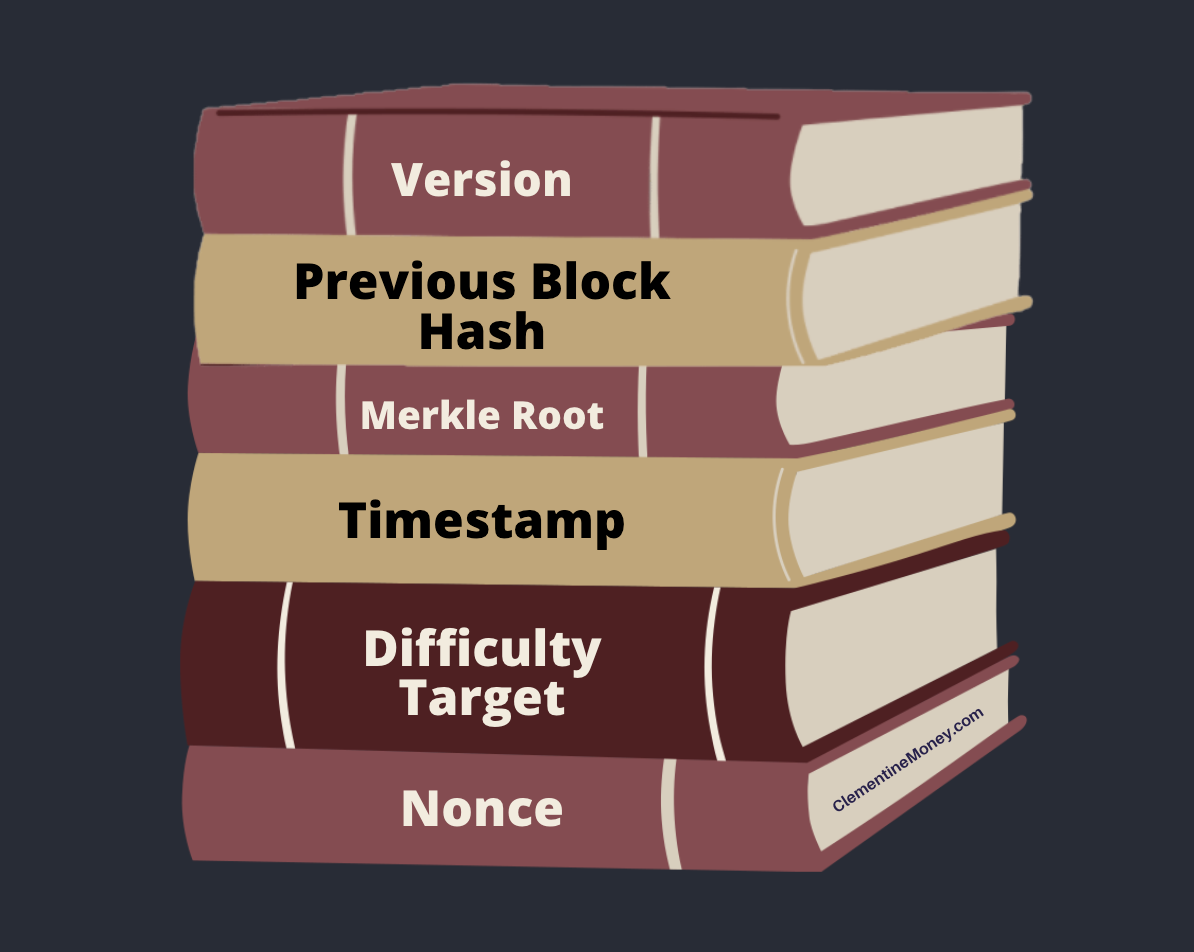
Next, Mallory's mining node sends its candidate block over to her mining ASIC and says "Find me a nonce that works for this difficulty target".

The Nonce

"Nonce" stands for "number used only once". Each block has a fixed size of one megabyte (MB). Within that finite space, there is room in the block header designated for a nonce, which miners' ASICs alter repeatedly to change the hash of the block. This is exactly the same exercise as the challenge above!

Miners compete in this hashing race, changing their respective nonces repeatedly until a specific target hash is achieved. Whoever wins this race will have their block validated and accepted by the Bitcoin network as Block #21. That miner's coinbase transaction will therefore be validated and they will receive the proceeds.

That is how miners receive their bitcoin rewards for mining!

Step 4: Adding Transactions

Hashing usually takes a long time (remember: ten minutes on average). In the meantime, Mallory can start adding transactions to her block from the mempool.

Bob's transactions now get scooped up by Mallory's mining node and added to her block. All the while, her ASIC is hashing away, and she hopes it will find her a nonce that produces a valid proof-of-work satisfying the difficulty target.

Fees

Bob sent 1 BTC to Alice, but he also paid a mining fee of 0.00001 BTC. He did this to incentivize miners like Mallory to include his transaction in a block. Bob could have paid a higher fee if his transaction was urgent, or he could have paid a lower fee if he didn't mind waiting. Most bitcoin wallets choose an average fee automatically so Bob won't have to waste time making that decision.

Mallory's mining node is programmed to optimize for selecting transactions that carry higher fees. After adding a transaction to its candidate block, Mallory's mining node will also include an instruction in the coinbase transaction to pay the attached fee to Mallory along with the 6.25 BTC reward.

That is how miners receive transaction fees for mining!

Step 5: Submitting Results

At last, Mallory's mining ASIC finds a valid proof-of-work, and her mining node submits its block full of transactions to the Bitcoin network to be verified!

Nodes on the network can quickly and easily see that Mallory's block contains valid transactions, a valid proof-of-work, and a valid block header. They therefore add Mallory's block to the blockchain as Block #21, and broadcast the result to all other nodes on the network. Other miners running their mining nodes receive Block #21, and the race is on to find a valid target hash for the next block (Block #22).

Bob's wallet will show his transaction has been confirmed. After three confirmations, his transaction is considered final and irreversible.

Summary

Proof-of-work (PoW) is just what it sounds like: proof that work has been done. "Work" refers to spent energy. PoW is self-evident and you see it every day: a hot coffee is proof-of-heating and footprints in the snow are proof-of-walking.

Adam Back's Hashcash from 1997 was the first major implementation of PoW in a distributed network, which used it to combat email spam. Satoshi Nakamoto's Bitcoin from 2008 requires miners to present PoW to the network before their mined blocks can be added to the blockchain. Both systems utilize a specific type of work called hashing, which involves randomly guessing inputs until an acceptable output is found. Hashes are costly to produce but easy to verify, making them an ideal form of PoW for bitcoin.

Nakamoto realized proof-of-work is the key to solving a longstanding paradox in distributed data systems, known as The Byzantine Generals' Problem. Each computer (node) must find a provably difficult target hash, recalibrated every two weeks to ensure blocks are generated every ten minutes on average. Nodes always choose the longest chain––a rule known now as Nakamoto Consensus, which ensures consensus with sufficient time passed and work done.

The bitcoin mining process consists of five steps:

1. A miner sets up a mining node and a mining ASIC
2. User transactions are broadcast from wallets to nodes' mempools
3. The miner constructs a candidate block and begins hashing for a target by altering a nonce within the block
4. Meanwhile, the miner adds transactions to the block from the mempool, often optimizing for transactions that pay the highest fee
5. The miner finds a valid PoW and submits their block full of transactions to the Bitcoin network to be confirmed, receiving the block reward and fees in return!

Share on Twitter

Additional Resources

1. [Email] Re: Bitcoin P2P e-cash paper by Satoshi Nakamoto
2. [Video] Byzantine Generals Problem by Mark Reddick
3. [Video] Bitcoin Q&A: The Mining Process by Andreas Antonopoulos

🍊 Found this valuable?

🎓 Ready to Test Your Knowledge?

Subscribe for free so you don't miss our next article!